Roadtrip to Ludolph van Ceulen

Today is March 14th (3/14), otherwise known as Pi Day!

Calculating Pi

To celebrate Pi Day people often try to come up with cool and interesting ways to calculate π, or to celebrate the number in weird ways.

Here is a great example by the excellent Matt Parker (from Stand-up Maths):

He’s using the “Isaac Newton”-way to calculate π by hand. This method was discovered by Isaac Newton and German mathematician Gottfried Wilhelm Leibniz in 1665. And it uses ‘infinite series’.

Before Newton

The method Newton used (infinite series) was mathematically superiour to all previous methods of calculating π.

That does raise a question: How did they calculate π before 1665?

First let’s take one step back, what exactly IS π? π is a mathematical constant: the ratio between a circle’s circumference and diameter. This means that if you have a circle with a diameter of 1, the circumference is π (~ 3.14159…).

Let’s try to come up with a very rough estimate what this ratio needs to be. What if we put our unit-circle with length 1 inside a square:

We can conclude that the circumference, and therefor π, is at most 4 x 1 = 4, this gives us the first upper bound.

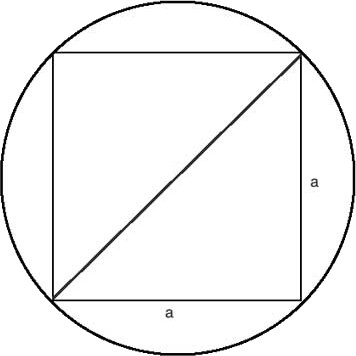
Now lets look at the other case, where the square fits inside the circle. In this case we can see that we have an equilateral triangle, with two sides a that make the square. The length of a is easy to calculate using Pythagoras theorom, the long side has a diameter of 1, this means a needs to be a^2 + a^2 = 1. If we rearrange everything we’ll come to the conclusion that a = sqrt(0.5).

This means that the circumference of the smaller square is 4 x sqrt(0.5) = ~ 2.82...

We can conclude that π lies somewhere between 4 and 2.82 🎉

Archimedes method

But can we do even better? Sure! What if, instead of placing our circle between two squares, we use pentagons, hexagons, or shapes with even more sides?

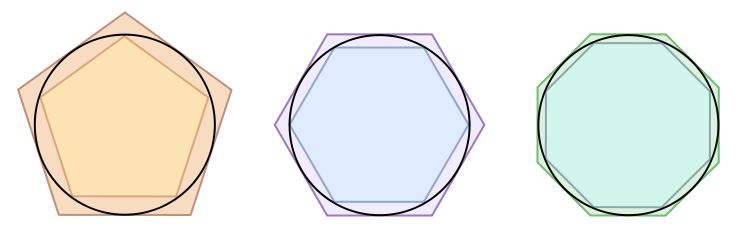
As you can see, the shape get more and more rounded. So the upper and lower bounds converge towards our beloved π!

This method is known as Archimedes method. Archimedes calculated, using a shape with 128 sides, that π had to be between 3.141 and 3.142.

Ludolph van Ceulen

Now it’s time to introduce our hero of today: Ludolph van Ceulen

Ludolph spend his entire life to improve the calculated value of π. Instead of using a 128-sided shape like Archimedes, he calculated π using shapes with up to millions of sides. Let that sink in, a shape with a million sides, by hand. By the time of his death van Ceulen managed to calculate π up to 35 digits, an incredible feat.

Ludolph was so pleased with his life goal that he requested the upper and lower bounds to be carved into his tombstone. Sadly the original tombstone went missing not long after his death. However a new tombstone was added to the famous St. Peter’s Church in Leiden (The Netherlands) in the year 2000.

Visiting Leiden

About a month ago, my girlfriend and I, bored in lockdown, decided to take a roadtrip and visit the church in Leiden to see the tombstone for ourselves.

And there it is, here is a better picture of the plaque:

I’ve tried to translate the plaque from ‘old Dutch’ into English and it reads something like:

Buried here is Mr. Ludolph van Ceulen.
He was a Dutch professor of Mathematics at the university of this city (Leiden).
Born in Hildesheim in the year 1540 at 28th of January.
Passed away 31st of December 1610.
During his life, through hard labour, he found the circle's circumference compared to the diameter to be...

If the diameter is 1
The circumference is at least:

3141592653589793238462643383279502881
-------------------------------------
100000000000000000000000000000000000

And at most:

3141592653589793238462643383279502891
-------------------------------------
100000000000000000000000000000000000

And if the diameter is 100000000000000000000000000000000000

The circumference is at least 
314159265358979323846264338327950288

And at most:
314159265358979323846264338327950289

He spend his entire life to improve the upper and lower bounds, using more and more sided shapes, up to millions of sides. He was also the last person to improve the records using this labour intensive method. The method co-discovered by Isaac Newton (using infinite series) proved to be much easier and faster to calculate. After that calculating π by using complex shapes was a thing of the past.

If you’re ever in Leiden, be sure to visit the church and pay respects to the incredible diligence of Ludolph van Ceulen.

Happy Pi Day!